${{\mathit t}}$-QUARK MASS
We first list the direct measurements of the top quark mass which employ the event kinematics and then list the measurements which extract a top quark mass from the measured ${{\mathit t}}{{\overline{\mathit t}}}$ cross-section using theory calculations. A discussion of the definition of the top quark mass in these measurements can be found in the review “The Top Quark.''
For earlier search limits see PDG 1996 , Physical Review D54 1 (1996). We no longer include a compilation of indirect top mass determinations from Standard Model Electroweak fits in the Listings (our last compilation can be found in the Listings of the 2007 partial update). For a discussion of current results see the reviews "The Top Quark" and "Electroweak Model and Constraints on New Physics."
For earlier search limits see PDG 1996 , Physical Review D54 1 (1996). We no longer include a compilation of indirect top mass determinations from Standard Model Electroweak fits in the Listings (our last compilation can be found in the Listings of the 2007 partial update). For a discussion of current results see the reviews "The Top Quark" and "Electroweak Model and Constraints on New Physics."
${{\mathit t}}$-Quark Mass (Direct Measurements)
INSPIRE PDGID:Q007TP
The following measurements extract a ${{\mathit t}}$-quark mass from the kinematics of ${{\mathit t}}{{\overline{\mathit t}}}$ events. They are sensitive to the top quark mass used in the MC generator that is usually interpreted as the pole mass, but the theoretical uncertainty in this interpretation is hard to quantify. See the review “The Top Quark” and references therein for more information.
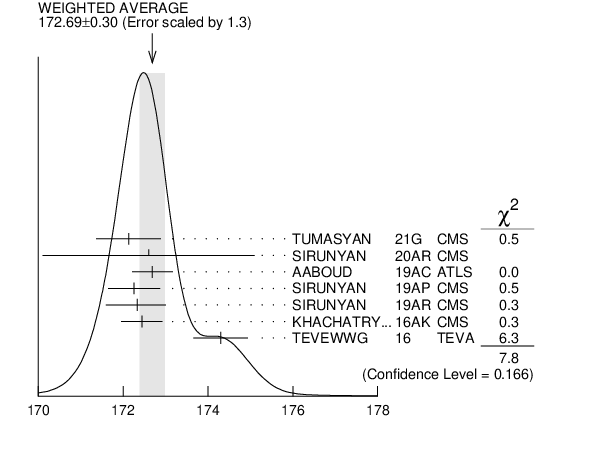
OUR AVERAGE of $172.69$ $\pm0.30$ (GeV) is an average of top mass measurements from LHC and Tevatron Runs. The latest Tevatron average, $174.30$ $\pm0.35$ $\pm0.54$ GeV, was provided by the Tevatron Electroweak Working Group (TEVEWWG).
OUR AVERAGE of $172.69$ $\pm0.30$ (GeV) is an average of top mass measurements from LHC and Tevatron Runs. The latest Tevatron average, $174.30$ $\pm0.35$ $\pm0.54$ GeV, was provided by the Tevatron Electroweak Working Group (TEVEWWG).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
${{\mathit t}}$-Quark Mass (Direct Measurements) (GeV) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| References: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Except where otherwise noted, content of the 2023 Review of Particle Physics is licensed under a Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0) license. The publication of the Review of Particle Physics is supported by US DOE, MEXT (Japan), INFN (Italy), JPS and CERN. Individual collaborators receive support for their PDG activities from their respective institutes or funding agencies. © 2023. See LBNL disclaimers.