pdgLive

${\mathit {\mathit s}}$-QUARK MASS

See the comment for the ${{\mathit u}}$ quark above.

We have normalized the $\overline{\rm{}MS}$ masses at a renormalization scale of $\mu $ = 2 GeV. Results quoted in the literature at $\mu $ = 1 GeV have been rescaled by dividing by $1.35$.

VALUE (MeV)

DOCUMENT ID

TECN

$\bf{ 93.5 \pm0.8}$

OUR EVALUATION

See the ideogram below.

$98.7$ $\pm2.4$ ${}^{+4.0}_{-3.2}$

LATT

$95.7$ $\pm2.5$ $\pm2.4$

LATT

$92.47$ $\pm0.69$

LATT

$93.85$ $\pm0.75$

LATT

$87.6$ $\pm6.0$

ANANTHANARAYA..

THEO

$99.6$ $\pm4.3$

LATT

$94.4$ $\pm2.3$

LATT

$94$ $\pm9$

THEO

$95.5$ $\pm1.1$ $\pm1.5$

LATT

• • We do not use the following data for averages, fits, limits, etc. • •

$93.6$ $\pm0.8$

LATT

$102$ $\pm3$ $\pm1$

LATT

$96.2$ $\pm2.7$

LATT

$95$ $\pm6$

LATT

$97.6$ $\pm2.9$ $\pm5.5$

LATT

$92.4$ $\pm1.5$

LATT

$92.2$ $\pm1.3$

LATT

$107.3$ $\pm11.7$

LATT

$105$ $\pm3$ $\pm9$

LATT

$102$ $\pm8$

THEO

$90.1$ ${}^{+17.2}_{-6.1}$

LATT

$105.6$ $\pm1.2$

LATT

$119.5$ $\pm9.3$

LATT

$105$ $\pm6$ $\pm7$

THEO

$111$ $\pm6$ $\pm10$

LATT

$119$ $\pm5$ $\pm8$

LATT

$92$ $\pm9$

THEO

$87$ $\pm6$

LATT

$104$ $\pm15$

THEO

${}\geq{}\text{ 71 }\pm4, {}\leq{}\text{ 151 }\pm14$

THEO

$96$ ${}^{+5}_{-3}$ ${}^{+16}_{-18}$

THEO

$81$ $\pm22$

THEO

$125$ $\pm28$

THEO

$93$ $\pm32$

THEO

$76$ $\pm8$

LATT

$116$ $\pm6$ $\pm0.65$

LATT

$84.5$ ${}^{+12}_{-1.7}$

LATT

$106$ $\pm2$ $\pm8$

LATT

$92$ $\pm9$ $\pm16$

LATT

$117$ $\pm17$

THEO

$103$ $\pm17$

THEO

¹

ALEXANDROU 2021 determines the quark mass using a lattice calculation of the meson and baryon masses with a twisted mass fermion action. The simulations are carried out using 2+1+1 dynamical quarks with ${\mathit m}_{{{\mathit u}}}$ = ${\mathit m}_{{{\mathit d}}}{}\not={\mathit m}_{{{\mathit s}}}{}\not={\mathit m}_{{{\mathit c}}}$, including gauge ensembles close to the physical pion point.

²

BRUNO 2020 determines the light quark mass using a lattice calculation with ${{\mathit n}_{{{f}}}}$ = 2+1 flavors of Wilson fermions. The scale has been set from ${{\mathit f}_{{{\pi}}}}$ and ${{\mathit f}_{{{K}}}}$. The tuning was done using the masses of the lightest (${{\mathit \pi}}$) and strange (${{\mathit K}}$) pseudoscalar mesons.

³	BAZAVOV 2018 determine the quark masses using a lattice computation with staggered fermions and four active quark flavors.

⁴

LYTLE 2018 combined with CHAKRABORTY 2015 determine ${{\overline{\mathit m}}_{{{s}}}}$(3 GeV) = $84.78$ $\pm0.65$ MeV from a lattice simulation with ${{\mathit n}_{{{f}}}}$ = 2+1+1 flavors. They also determine the quoted value ${{\overline{\mathit m}}_{{{s}}}}$(2 GeV) for ${{\mathit n}_{{{f}}}}$ = 4 dynamical flavors.

⁵	ANANTHANARAYAN 2016 determine ${{\overline{\mathit m}}_{{{s}}}}$(2 GeV) = $106.70$ $\pm9.36$ MeV and $74.47$ $\pm7.77$ MeV from fits to ALEPH and OPAL ${{\mathit \tau}}$ decay data, respectively. We have used the weighted average of the two.

⁶

CARRASCO 2014 is a lattice QCD computation of light quark masses using 2 + 1 + 1 dynamical quarks, with ${{\mathit m}_{{{u}}}}$ = ${{\mathit m}_{{{d}}}}{}\not=$ ${{\mathit m}_{{{s}}}}{}\not=$ ${{\mathit m}_{{{c}}}}$. The ${\mathit {\mathit u}}$ and ${\mathit {\mathit d}}$ quark masses are obtained separately by using the ${{\mathit K}}$ meson mass splittings and lattice results for the electromagnetic contributions.

⁷	ARTHUR 2013 is a lattice computation using 2+1 dynamical domain wall fermions. Masses at ${{\mathit \mu}}$ = 3 GeV have been converted to ${{\mathit \mu}}$ = 2 GeV using conversion factors given in their paper.

⁸	BODENSTEIN 2013 determines ${\mathit m}_{{{\mathit s}}}$ from QCD finite energy sum rules, and the perturbative computation of the pseudoscalar correlator to five-loop order.

⁹	DURR 2011 determine quark mass from a lattice computation of the meson spectrum using ${{\mathit n}_{{{f}}}}$ = 2 + 1 dynamical flavors. The lattice simulations were done at the physical quark mass, so that extrapolation in the quark mass was not needed.

¹⁰

CHAKRABORTY 2015 is a lattice QCD computation that determines ${\mathit m}_{{{\mathit c}}}$ and ${\mathit m}_{{{\mathit c}}}/{\mathit m}_{{{\mathit s}}}$ using pseudoscalar mesons masses tuned on gluon field configurations with 2+1+1 dynamical flavors of HISQ quarks with ${{\mathit u}}/{{\mathit d}}$ masses down to the physical value.

¹¹	FRITZSCH 2012 determine ${\mathit m}_{{{\mathit s}}}$ using a lattice computation with ${{\mathit n}_{{{f}}}}$ = 2 dynamical flavors.

¹²	AOKI 2011A determine quark masses from a lattice computation of the hadron spectrum using ${{\mathit n}_{{{f}}}}$ = 2 + 1 dynamical flavors of domain wall fermions.

¹³	BLOSSIER 2010 determines quark masses from a computation of the hadron spectrum using ${{\mathit n}_{{{f}}}}$=2 dynamical twisted-mass Wilson fermions.

¹⁴	BLUM 2010 determines light quark masses using a QCD plus QED lattice computation of the electromagnetic mass splittings of the low-lying hadrons. The lattice simulations use 2+1 dynamical quark flavors.

¹⁵

DAVIES 2010 and MCNEILE 2010 determine ${{\overline{\mathit m}}_{{{c}}}}({{\mathit \mu}})/{{\overline{\mathit m}}_{{{s}}}}({{\mathit \mu}}$) = $11.85$ $\pm0.16$ using a lattice computation with ${{\mathit n}_{{{f}}}}$ = 2 + 1 dynamical fermions of the pseudoscalar meson masses. Mass ${\mathit m}_{{{\mathit s}}}$ is obtained from this using the value of ${\mathit m}_{{{\mathit c}}}$ from ALLISON 2008 or MCNEILE 2010.

¹⁶	ALLTON 2008 use a lattice computation of the ${{\mathit \pi}}$, ${{\mathit K}}$, and ${{\mathit \Omega}}$ masses with 2+1 dynamical flavors of domain wall quarks, and non-perturbative renormalization.

¹⁷	BLOSSIER 2008 use a lattice computation of pseudoscalar meson masses and decay constants with 2 dynamical flavors and non-perturbative renormalization.

¹⁸	DOMINGUEZ 2008A make determination from QCD finite energy sum rules for the pseudoscalar two-point function computed to order $\alpha {}^{4}_{s}$.

¹⁹	ISHIKAWA 2008 use a lattice computation of the light meson spectrum with 2+1 dynamical flavors of $\cal O(\mathit a$) improved Wilson quarks, and one-loop perturbative renormalization.

²⁰	NAKAMURA 2008 do a lattice computation using quenched domain wall fermions and non-perturbative renormalization.

²¹	BLUM 2007 determine quark masses from the pseudoscalar meson masses using a QED plus QCD lattice computation with two dynamical quark flavors.

²²	CHETYRKIN 2006 use QCD sum rules in the pseudoscalar channel to order ${{\mathit \alpha}_{{{s}}}^{4}}$.

²³

GOCKELER 2006 use an unquenched lattice computation of the axial Ward Identity with ${{\mathit n}_{{{f}}}}$ = 2 dynamical light quark flavors, and non-perturbative renormalization, to obtain ${{\overline{\mathit m}}_{{{s}}}}$(2 GeV) = $111$ $\pm6$ $\pm4$ $\pm6$ MeV, where the first error is statistical, the second and third are systematic due to the fit range and force scale uncertainties, respectively. We have combined the systematic errors linearly.

²⁴	GOCKELER 2006A use an unquenched lattice computation of the pseudoscalar meson masses with ${{\mathit n}_{{{f}}}}$ = 2 dynamical light quark flavors, and non-perturbative renormalization.

²⁵	JAMIN 2006 determine ${{\overline{\mathit m}}_{{{s}}}}$(2 GeV) from the spectral function for the scalar ${{\mathit K}}{{\mathit \pi}}$ form factor.

²⁶	MASON 2006 extract light quark masses from a lattice simulation using staggered fermions with an improved action, and three dynamical light quark flavors with degenerate ${\mathit {\mathit u}}$ and ${\mathit {\mathit d}}$ quarks. Perturbative corrections were included at NNLO order.

²⁷	NARISON 2006 uses sum rules for ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ hadrons to order ${{\mathit \alpha}_{{{s}}}^{3}}$.

²⁸	NARISON 2006 obtains the quoted range from positivity of the spectral functions.

²⁹

BAIKOV 2005 determines ${{\overline{\mathit m}}_{{{s}}}}({{\mathit M}_{{{\tau}}}}$) = $100$ ${}^{+5}_{-3}{}^{+17}_{-19}$ from sum rules using the strange spectral function in ${{\mathit \tau}}$ decay. The computations were done to order ${{\mathit \alpha}_{{{s}}}^{3}}$, with an estimate of the ${{\mathit \alpha}_{{{s}}}^{4}}$ terms. We have converted the result to ${{\mathit \mu}}$ = 2 GeV.

³⁰	GAMIZ 2005 determines ${{\overline{\mathit m}}_{{{s}}}}$(2 GeV) from sum rules using the strange spectral function in ${{\mathit \tau}}$ decay. The computations were done to order ${{\mathit \alpha}_{{{s}}}^{2}}$, with an estimate of the ${{\mathit \alpha}_{{{s}}}^{3}}$ terms.

³¹	GORBUNOV 2005 use hadronic tau decays to N3LO, including power corrections.

³²	NARISON 2005 determines ${{\overline{\mathit m}}_{{{s}}}}$(2 GeV) from sum rules using the strange spectral function in ${{\mathit \tau}}$ decay. The computations were done to order ${{\mathit \alpha}_{{{s}}}^{3}}$.

³³	AUBIN 2004 perform three flavor dynamical lattice calculation of pseudoscalar meson masses, with one-loop perturbative renormalization constant.

³⁴

AOKI 2003 uses quenched lattice simulation of the meson and baryon masses with degenerate light quarks. The extrapolations are done using quenched chiral perturbation theory. Determines m$_{s}=113.8$ $\pm2.3$ ${}^{+5.8}_{-2.9}$ using ${{\mathit K}}$ mass as input and m$_{s}=142.3$ $\pm5.8$ ${}^{+22}_{-0}$ using ${{\mathit \phi}}$ mass as input. We have performed a weighted average of these values.

³⁵	AOKI 2003B uses lattice simulation of the meson and baryon masses with two dynamical light quarks. Simulations are performed using the $\cal O(\mathit a$) improved Wilson action.

³⁶	BECIREVIC 2003 perform quenched lattice computation using the vector and axial Ward identities. Uses $\cal O(\mathit a$) improved Wilson action and nonperturbative renormalization. They also quote ${{\overline{\mathit m}}}$/m$_{s}=24.3$ $\pm0.2$ $\pm0.6$.

³⁷	CHIU 2003 determines quark masses from the pion and kaon masses using a lattice simulation with a chiral fermion action in quenched approximation.

³⁸	GAMIZ 2003 determines ${\mathit m}_{{{\mathit s}}}$ from SU(3) breaking in the ${{\mathit \tau}}~$hadronic width. The value of $\mathit V_{{{\mathit u}} {{\mathit s}}}$ is chosen to satisfy CKM unitarity.

³⁹	GAMIZ 2003 determines ${\mathit m}_{{{\mathit s}}}$ from SU(3) breaking in the ${{\mathit \tau}}~$hadronic width. The value of $\mathit V_{{{\mathit u}} {{\mathit s}}}$ is taken from the PDG.

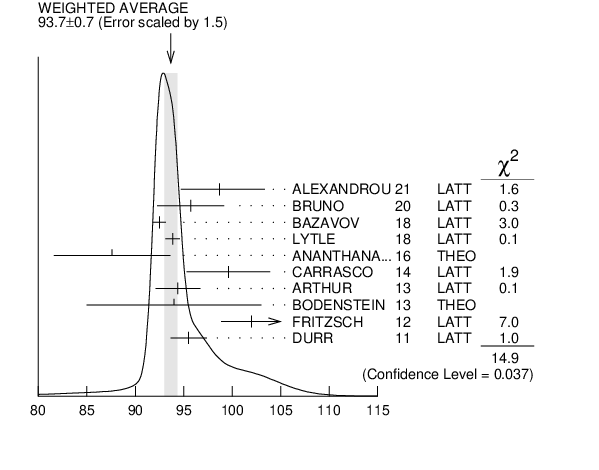
${\mathit {\mathit s}}$-QUARK MASS (MeV)

Except where otherwise noted, content of the 2024 Review of Particle Physics is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. The publication of the Review of Particle Physics is supported by US DOE, MEXT (Japan), INFN (Italy) and CERN. Individual collaborators receive support for their PDG activities from their respective institutes or funding agencies. © 2024. See LBNL disclaimers.