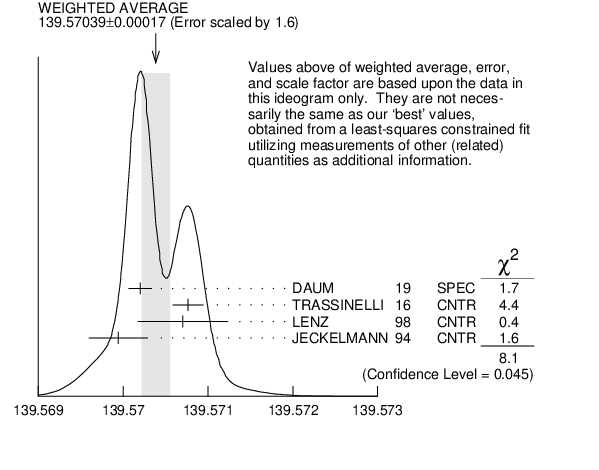
The most accurate charged pion mass measurements are based upon x-ray wavelength measurements for transitions in ${{\mathit \pi}^{-}}$-mesonic atoms. The observed line is the blend of three components, corresponding to different K-shell occupancies. JECKELMANN 1994 revisits the occupancy question, with the conclusion that two sets of occupancy ratios, resulting in two different pion masses (Solutions A and B), are equally probable. We choose the higher Solution$~$B since only this solution is consistent with a positive mass-squared for the muon neutrino, given the precise muon momentum measurements now available (DAUM 1991 , ASSAMAGAN 1994 , and ASSAMAGAN 1996 ) for the decay of pions at rest. Earlier mass determinations with pi-mesonic atoms may have used incorrect K-shell screening corrections.

Measurements with an error of $>0.005$ MeV have been omitted from this Listing.

VALUE (MeV) DOCUMENT ID TECN CHG  COMMENT $\bf{ 139.57039 \pm0.00018}$ OUR FIT  Error includes scale factor of 1.8. $\bf{ 139.57039 \pm0.00017}$ OUR AVERAGE  Error includes scale factor of 1.6.  See the ideogram below. $139.57021$ $\pm0.00014$ 1 DAUM 2019 SPEC ${{\mathit \pi}^{+}}$ $\rightarrow$ ${{\mathit \mu}^{+}}{{\mathit \nu}_{{\mu}}}$ $139.57077$ $\pm0.00018$ 2 TRASSINELLI 2016 CNTR X-ray transitions in pionic N2 $139.57071$ $\pm0.00053$ 3 LENZ 1998 CNTR - pionic -atoms gas target $139.56995$ $\pm0.00035$ 4 JECKELMANN 1994 CNTR - ${{\mathit \pi}^{-}}$ atom, Soln.$~$B • • We do not use the following data for averages, fits, limits, etc. • • $139.57022$ $\pm0.00014$ 5 ASSAMAGAN 1996 SPEC + ${{\mathit \pi}^{+}}$ $\rightarrow$ ${{\mathit \mu}^{+}}{{\mathit \nu}_{{\mu}}}$ $139.56782$ $\pm0.00037$ 6 JECKELMANN 1994 CNTR - ${{\mathit \pi}^{-}}$ atom, Soln.$~$A $139.56996$ $\pm0.00067$ 7 DAUM 1991 SPEC + ${{\mathit \pi}^{+}}$ $\rightarrow$ ${{\mathit \mu}^{+}}{{\mathit \nu}}$ $139.56752$ $\pm0.00037$ 8 JECKELMANN 1986 B CNTR - Mesonic atoms $139.5704$ $\pm0.0011$ 7 ABELA 1984 SPEC + See DAUM 1991 $139.5664$ $\pm0.0009$ 9 LU 1980 CNTR - Mesonic atoms $139.5686$ $\pm0.0020$ CARTER 1976 CNTR - Mesonic atoms $139.5660$ $\pm0.0024$ 9, 10 MARUSHENKO 1976 CNTR - Mesonic atoms 1  DAUM 2019 value is based on their previous (1991+1996) measurements of the ${{\mathit \mu}^{+}}$ momentum of $29.79200$ $\pm0.00011$ MeV for ${{\mathit \pi}^{+}}$ decay at rest. It also uses ${\mathit m}_{{{\mathit \mu}}}$ = $105.6583745$ $\pm0.0000024$ MeV, and assumes conservatively ${\mathit m}_{{{\mathit \nu}_{{\mu}}}}$ = $2.0$ $\pm2.0$ MeV. It is the most precise charged pion mass determination. 2  TRASSINELLI 2016 use the muonic oxygen line for online energy calibration of the pionic line. 3  LENZ 1998 result does not suffer K-electron configuration uncertainties as does JECKELMANN 1994 . 4  JECKELMANN 1994 Solution B (dominant 2-electron K-shell occupancy), chosen for consistency with positive ${{\mathit m}^{2}}_{{{\mathit \nu}_{{\mu}}}}$. 5  ASSAMAGAN 1996 measures the ${{\mathit \mu}^{+}}$ momentum ${{\mathit p}_{{\mu}}}$ in ${{\mathit \pi}^{+}}$ $\rightarrow$ ${{\mathit \mu}^{+}}{{\mathit \nu}_{{\mu}}}$ decay at rest to be $29.79200$ $\pm0.00011$ MeV/$\mathit c$. Combined with the ${{\mathit \mu}^{+}}$ mass and the assumption ${\mathit m}_{{{\mathit \nu}_{{\mu}}}}$ = 0, this gives the ${{\mathit \pi}^{+}}$ mass above; if ${\mathit m}_{{{\mathit \nu}_{{\mu}}}}>~$0, ${\mathit m}_{{{\mathit \pi}^{+}}}$ given above is a lower limit. Combined instead with ${\mathit m}_{{{\mathit \mu}}}$ and (assuming $\mathit CPT$) the ${{\mathit \pi}^{-}}$ mass of JECKELMANN 1994 , $\mathit p_{{{\mathit \mu}}}$ gives an upper limit on ${\mathit m}_{{{\mathit \nu}_{{\mu}}}}$ (see the ${{\mathit \nu}_{{\mu}}}$). 6  JECKELMANN 1994 Solution A (small 2-electron K-shell occupancy) in combination with either the DAUM 1991 or ASSAMAGAN 1994 pion decay muon momentum measurement yields a significantly negative ${{\mathit m}^{2}}_{{{\mathit \nu}_{{\mu}}}}$. It is accordingly not used in our fits. 7  The DAUM 1991 value includes the ABELA 1984 result. The value is based on a measurement of the ${{\mathit \mu}^{+}}$ momentum for ${{\mathit \pi}^{+}}$ decay at rest, ${{\mathit p}_{{\mu}}}$ = $29.79179$ $\pm0.00053$ MeV, uses ${\mathit m}_{{{\mathit \mu}}}$ = $105.658389$ $\pm0.000034$ MeV, and assumes that ${\mathit m}_{{{\mathit \nu}_{{\mu}}}}$ = 0. The last assumption means that in fact the value is a lower limit. 8  JECKELMANN 1986B gives ${\mathit m}_{{{\mathit \pi}}}/{\mathit m}_{{{\mathit e}}}$ = 273.12677(71). We use ${\mathit m}_{{{\mathit e}}}$ = 0.51099906(15) MeV from COHEN 1987 . The authors note that two solutions for the probability distribution of K-shell occupancy fit equally well, and use other data to choose the lower of the two possible ${{\mathit \pi}^{\pm}}$ masses. 9  These values are scaled with a new wavelength-energy conversion factor $\mathit V\lambda $ = $1.23984244(37){\times }10^{-6}$ eV m from COHEN 1987 . The LU 1980 screening correction relies upon a theoretical calculation of inner-shell refilling rates. 10  This MARUSHENKO 1976 value used at the authors' request to use the accepted set of calibration ${{\mathit \gamma}}$ energies. Error increased from 0.0017 MeV to include QED calculation error of 0.0017 MeV (12 ppm).

${{\mathit \pi}^{\pm}}$ mass (MeV)

References:

DAUM 2019 PL B796 11 The charged and neutral pion masses revisited TRASSINELLI 2016 PL B759 583 Measurement of the Charged Pion Mass using X-ray Spectroscopy of Exotic Atoms LENZ 1998 PL B416 50 A New Determination of the Mass of the Charged Pion ASSAMAGAN 1996 PR D53 6065 Upper Limit of the ${{\mathit \nu}_{{\mu}}}$ Mass and Charged Pion Mass from Momentum Analysis of a Surface Muon Beam JECKELMANN 1994 PL B335 326 The Mass of the Negative Pion DAUM 1991 PL B265 425 New Precision Measurement of the Muon Momentum in Pion Decay at Rest JECKELMANN 1986B NP A457 709 New Precision Determination of the ${{\mathit \pi}^{-}}$ Mass from Pionic X Rays Also PRL 56 1444 New Precision Determination of the ${{\mathit \pi}^{-}}$ Mass from Pionic X Rays ABELA 1984 PL 146B 431 Precision Measurement of the Muon Momentum in Pion Decay at Rest Also PL 74B 126 Precision Measurement of the Muon Momentum in Pion Decay at Rest Also PR D20 2692 Precision Measurement of the Muon Momentum in Pion Decay at Rest LU 1980 PRL 45 1066 New High Accuracy Measurement of the Pionic Mass CARTER 1976 PRL 37 1380 A New Determination of the ${{\mathit \pi}^{-}}$ Mass from Pionic Atom Transition Energies MARUSHENKO 1976 JETPL 23 72 New Measurement of ${{\mathit \pi}^{-}}$ Mass Also Private Comm. Private Communication Also Private Comm. Private Communication