${{\mathit t}}$-QUARK MASS

We first list the direct measurements of the top quark mass which employ the event kinematics and then list the measurements which extract a top quark mass from the measured ${{\mathit t}}{{\overline{\mathit t}}}$ cross-section using theory calculations. A discussion of the definition of the top quark mass in these measurements can be found in the review “The Top Quark.''
For earlier search limits see PDG 1996, Physical Review D54 1 (1996). We no longer include a compilation of indirect top mass determinations from Standard Model Electroweak fits in the Listings (our last compilation can be found in the Listings of the 2007 partial update). For a discussion of current results see the reviews "The Top Quark" and "Electroweak Model and Constraints on New Physics."

${{\mathit t}}$-Quark Mass (Direct Measurements)

INSPIRE   JSON  (beta) PDGID:
Q007TP
The following measurements extract a ${{\mathit t}}$-quark mass from the kinematics of ${{\mathit t}}{{\overline{\mathit t}}}$ events. They are sensitive to the top quark mass used in the MC generator that is usually interpreted as the pole mass, but the theoretical uncertainty in this interpretation is hard to quantify. See the review “The Top Quark” and references therein for more information.

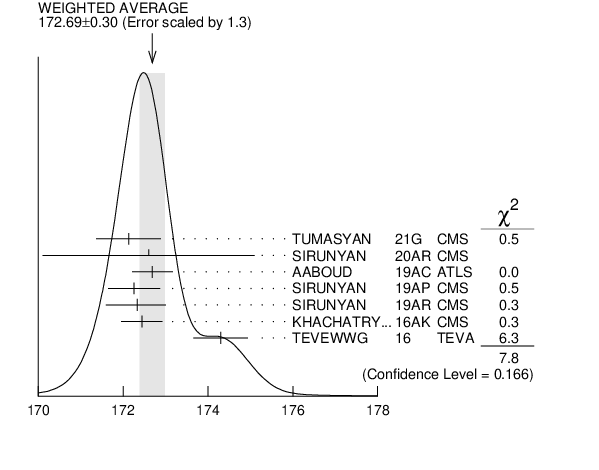
OUR AVERAGE of $172.56$ $\pm0.31$ (GeV) is an average of top mass measurements from LHC and Tevatron Runs. The latest Tevatron average, $174.30$ $\pm0.35$ $\pm0.54$ GeV, was provided by the Tevatron Electroweak Working Group (TEVEWWG).

VALUE (GeV) DOCUMENT ID TECN  COMMENT
$\bf{ 172.56 \pm0.31}$ OUR AVERAGE  Error includes scale factor of 1.6.  See the ideogram below.
$172.52$ $\pm0.14$ $\pm0.30$ 1
HAYRAPETYAN
2024F
 LHC ATLAS+CMS combined
$174.41$ $\pm0.39$ $\pm0.71$ 2
AAD
2023N
 ATLS leptonic invariant mass in ${{\mathit \ell}}$+jets channel
$171.77$ $\pm0.37$ 3
TUMASYAN
2023BB
 CMS ${{\mathit \ell}}$ +${}\geq{}$4j (2${{\mathit b}}$)
$173.06$ $\pm0.24$ $\pm0.80$ 4
TUMASYAN
2023Z
 CMS boosted top; ${{\mathit \ell}}$+jets channel
$172.13$ ${}^{+0.76}_{-0.77}$ 5
TUMASYAN
2021G
 CMS ${{\mathit t}}$-channel single top production
$172.6$ $\pm2.5$ 6
SIRUNYAN
2020AR
 CMS jet mass from boosted top
$172.34$ $\pm0.20$ $\pm0.70$ 7
SIRUNYAN
2019AP
 CMS ${}\geq{}$6 jets (${}\geq{}2{{\mathit b}}$)
$172.33$ $\pm0.14$ ${}^{+0.66}_{-0.72}$ 8
SIRUNYAN
2019AR
 CMS dilepton channel (${{\mathit e}}{{\mathit \mu}}$, 2${{\mathit e}}$, 2${{\mathit \mu}}$)
$174.30$ $\pm0.35$ $\pm0.54$ 9
TEVEWWG
2016
TEVA Tevatron combination
• • We do not use the following data for averages, fits, limits, etc. • •
$172.08$ $\pm0.39$ $\pm0.82$ 10
AABOUD
2019AC
 ATLS ${{\mathit \ell}}$ +${}\geq{}$4j (2${{\mathit b}}$)
$172.69$ $\pm0.25$ $\pm0.41$ 11
AABOUD
2019AC
 ATLS 7, 8 TeV ATLAS combination, superseded by HAYRAPETYAN 2024F
$172.26$ $\pm0.07$ $\pm0.61$ 12
SIRUNYAN
2019AP
 CMS lepton+jets, all-jets channels
$172.25$ $\pm0.08$ $\pm0.62$ 13
SIRUNYAN
2018DE
 CMS ${{\mathit \ell}}$ +${}\geq{}$4j (2${{\mathit b}}$)
$173.72$ $\pm0.55$ $\pm1.01$ 14
AABOUD
2017AH
 ATLS ${}\geq{}$5 jets (2${{\mathit b}}$)
$174.95$ $\pm0.40$ $\pm0.64$ 15
ABAZOV
2017B
 D0 ${{\mathit \ell}}$ + jets and dilepton channels
$172.95$ $\pm0.77$ ${}^{+0.97}_{-0.93}$ 16
SIRUNYAN
2017L
 CMS ${{\mathit t}}$-channel single top production
$170.8$ $\pm9.0$ 17
SIRUNYAN
2017N
 CMS jet mass in highly-boosted ${{\mathit t}}{{\overline{\mathit t}}}$ events
$172.22$ $\pm0.18$ ${}^{+0.89}_{-0.93}$ 18
SIRUNYAN
2017O
 CMS Dilepton channel
$172.99$ $\pm0.41$ $\pm0.74$ 19
AABOUD
2016T
 ATLS dilepton channel
$172.84$ $\pm0.34$ $\pm0.61$ 20
AABOUD
2016T
 ATLS combination of ATLAS
$173.32$ $\pm1.36$ $\pm0.85$ 21
ABAZOV
2016
D0 ${{\mathit \ell}}{{\mathit \ell}}$ + $\not E_T$ +${}\geq{}$2j (${}\geq{}2{{\mathit b}}$)
$173.93$ $\pm1.61$ $\pm0.88$ 22
ABAZOV
2016D
 D0 ${{\mathit \ell}}{{\mathit \ell}}$ + $\not E_T$ +${}\geq{}$2j (${}\geq{}2{{\mathit b}}$)
$172.35$ $\pm0.16$ $\pm0.48$ 23, 24
KHACHATRYAN
2016AK
 CMS ${{\mathit \ell}}$ +${}\geq{}$4j (2${{\mathit b}}$)
$172.32$ $\pm0.25$ $\pm0.59$ 23, 24
KHACHATRYAN
2016AK
 CMS ${}\geq{}$6 jets (2${{\mathit b}}$)
$172.82$ $\pm0.19$ $\pm1.22$ 23, 25
KHACHATRYAN
2016AK
 CMS (${{\mathit e}}{{\mathit e}}/{{\mathit \mu}}{{\mathit \mu}})+\not E_T+{}\geq{}2{{\mathit b}},{{\mathit e}}{{\mathit \mu}}+{}\geq{}2{{\mathit b}}$
$172.44$ $\pm0.13$ $\pm0.47$ 26
KHACHATRYAN
2016AK
 CMS 7, 8 TeV CMS combination, superseded by HAYRAPETYAN 2024F
$173.68$ $\pm0.20$ ${}^{+1.58}_{-0.97}$ 27
KHACHATRYAN
2016AL
 CMS semi- + di-leptonic channels
$173.5$ $\pm3.0$ $\pm0.9$ 28
KHACHATRYAN
2016CB
 CMS ${{\mathit t}}$ $\rightarrow$ ( ${{\mathit W}}$ $\rightarrow$ ${{\mathit \ell}}{{\mathit \nu}}$) ( ${{\mathit b}}$ $\rightarrow$ ${{\mathit J / \psi}}{{\mathit X}}$ $\rightarrow$ ${{\mathit \mu}^{+}}{{\mathit \mu}^{-}}{{\mathit X}}$)
$175.1$ $\pm1.4$ $\pm1.2$ 29
AAD
2015AW
 ATLS small $\not E_T$, ${}\geq{}$6 jets (2${{\mathit b}}$-tag)
$172.99$ $\pm0.48$ $\pm0.78$ 30
AAD
2015BF
 ATLS ${{\mathit \ell}}$ + jets and dilepton
$171.5$ $\pm1.9$ $\pm2.5$ 31
AALTONEN
2015D
 CDF ${{\mathit \ell}}{{\mathit \ell}}$ + $\not E_T$ +${}\geq{}$2j
$175.07$ $\pm1.19$ ${}^{+1.55}_{-1.58}$ 32
AALTONEN
2014N
 CDF small $\not E_T$, $6 - 8$ jets (${}\geq{}1{{\mathit b}}$-tag)
$174.98$ $\pm0.58$ $\pm0.49$ 33
ABAZOV
2014C
 D0 ${{\mathit \ell}}$ + $\not E_T$ + 4 jets (${}\geq{}$1 ${{\mathit b}}$-tag)
$173.49$ $\pm0.69$ $\pm1.21$ 34
CHATRCHYAN
2014C
 CMS ${}\geq{}$6 jets (${}\geq{}$2 ${{\mathit b}}$-tag)
$173.93$ $\pm1.64$ $\pm0.87$ 35
AALTONEN
2013H
 CDF $\not E_T$ + ${}\geq{}$4 jets (${}\geq{}$1 b)
$173.9$ $\pm0.9$ ${}^{+1.7}_{-2.1}$ 36
CHATRCHYAN
2013S
 CMS ${{\mathit \ell}}{{\mathit \ell}}+\not E_T+{}\geq{}2{{\mathit b}}$-tag (MT2$_{(T)}$)
$174.5$ $\pm0.6$ $\pm2.3$ 37
AAD
2012I
 ATLS ${{\mathit \ell}}+\not E_T+{}\geq{}$4 jets (${}\geq{}$1 ${{\mathit b}}$), MT
$172.85$ $\pm0.71$ $\pm0.85$ 38
AALTONEN
2012AI
 CDF ${{\mathit \ell}}+\not E_T+{}\geq{}$4j (0,1,2${{\mathit b}}$) template
$172.7$ $\pm9.3$ $\pm3.7$ 39
AALTONEN
2012AL
 CDF ${{\mathit \tau}_{{{h}}}}$ + $\not E_T$ +4j (${}\geq{}1{{\mathit b}}$)
$173.18$ $\pm0.56$ $\pm0.75$ 40
AALTONEN
2012AP
 TEVA CDF, D0 combination
$172.5$ $\pm1.4$ $\pm1.5$ 41
AALTONEN
2012G
 CDF $6 - 8$ jets with ${}\geq{}$1 ${{\mathit b}}$
$173.7$ $\pm2.8$ $\pm1.5$ 42
ABAZOV
2012AB
 D0 ${{\mathit \ell}}{{\mathit \ell}}$ + $\not E_T$ +${}\geq{}$2 j (${{\mathit \nu}}$WT)
$173.9$ $\pm1.9$ $\pm1.6$ 43
ABAZOV
2012AB
 D0 ${{\mathit \ell}}{{\mathit \ell}}+\not E_T+{}\geq{}$2j (${{\mathit \nu}}$WT+MWT)
$172.5$ $\pm0.4$ $\pm1.5$ 44
CHATRCHYAN
2012BA
 CMS ${{\mathit \ell}}{{\mathit \ell}}+\not E_T+{}\geq{}$2j (${}\geq{}1{{\mathit b}}$), AMWT
$173.49$ $\pm0.43$ $\pm0.98$ 45
CHATRCHYAN
2012BP
 CMS ${{\mathit \ell}}+\not E_T+{}\geq{}$4j (${}\geq{}2{{\mathit b}}$)
$172.4$ $\pm1.4$ $\pm1.3$ 46
AALTONEN
2011AC
 CDF ${{\mathit \ell}}$ + $\not E_T$ + 4 jets (${}\geq{}$1 ${{\mathit b}}$-tag)
$172.3$ $\pm2.4$ $\pm1.0$ 47
AALTONEN
2011AK
 CDF Repl. by AALTONEN 2013H
$172.1$ $\pm1.1$ $\pm0.9$ 48
AALTONEN
2011E
 CDF ${{\mathit \ell}}$ + jets and dilepton
$176.9$ $\pm8.0$ $\pm2.7$ 49
AALTONEN
2011T
 CDF ${{\mathit \ell}}$ + $\not E_T$ + 4 jets (${}\geq{}$1 ${{\mathit b}}$-tag), $p_T({{\mathit \ell}}$) shape
$174.94$ $\pm0.83$ $\pm1.24$ 50
ABAZOV
2011P
 D0 ${{\mathit \ell}}$ + $\not E_T$ + 4 jets (${}\geq{}$1 ${{\mathit b}}$-tag)
$174.0$ $\pm1.8$ $\pm2.4$ 51
ABAZOV
2011R
 D0 dilepton + $\not E_T$ +${}\geq{}$2 jets
$175.5$ $\pm4.6$ $\pm4.6$ 52
CHATRCHYAN
2011F
 CMS dilepton + $\not E_T$ + jets
$173.0$ $\pm0.9$ $\pm0.9$ 53
AALTONEN
2010AE
 CDF ${{\mathit \ell}}$ + $\not E_T$ + 4 jets (${}\geq{}$1 ${{\mathit b}}$-tag), ME method
$169.3$ $\pm2.7$ $\pm3.2$ 54
AALTONEN
2010C
 CDF dilepton + ${{\mathit b}}$-tag (MT2+NWA)
$170.7$ $\pm6.3$ $\pm2.6$ 55
AALTONEN
2010D
 CDF ${{\mathit \ell}}$ + $\not E_T$ + 4 jets (${{\mathit b}}$-tag)
$174.8$ $\pm2.4$ ${}^{+1.2}_{-1.0}$ 56
AALTONEN
2010E
 CDF ${}\geq{}$6 jets, vtx ${{\mathit b}}$-tag
$180.5$ $\pm12.0$ $\pm3.6$ 57
AALTONEN
2009AK
 CDF ${{\mathit \ell}}$ + $\not E_T$ + jets (soft ${{\mathit \mu}}$ b-tag)
$172.7$ $\pm1.8$ $\pm1.2$ 58
AALTONEN
2009J
 CDF ${{\mathit \ell}}$ + $\not E_T$ + 4 jets (${{\mathit b}}$-tag)
$171.1$ $\pm3.7$ $\pm2.1$ 59
AALTONEN
2009K
 CDF 6 jets, vtx ${{\mathit b}}$-tag
$171.9$ $\pm1.7$ $\pm1.1$ 60
AALTONEN
2009L
 CDF ${{\mathit \ell}}$ + jets, ${{\mathit \ell}}{{\mathit \ell}}$ + jets
$171.2$ $\pm2.7$ $\pm2.9$ 61
AALTONEN
2009O
 CDF dilepton
$165.5$ ${}^{+3.4}_{-3.3}$ $\pm3.1$ 62
AALTONEN
2009X
 CDF ${{\mathit \ell}}{{\mathit \ell}}$ + $\not E_T$ (${{\mathit \nu}}{{\mathit \phi}}$ weighting)
$174.7$ $\pm4.4$ $\pm2.0$ 63
ABAZOV
2009AH
 D0 dilepton + ${{\mathit b}}$-tag (${{\mathit \nu}}$WT+MWT)
$170.7$ ${}^{+4.2}_{-3.9}$ $\pm3.5$ 64, 65
AALTONEN
2008C
 CDF dilepton, $\sigma _{{{\mathit t}} {{\overline{\mathit t}}}}$ constrained
$171.5$ $\pm1.8$ $\pm1.1$ 66
ABAZOV
2008AH
 D0 ${{\mathit \ell}}$ + $\not E_T$ + 4 jets
$177.1$ $\pm4.9$ $\pm4.7$ 67, 68
AALTONEN
2007
CDF 6 jets with ${}\geq{}$1 ${{\mathit b}}$ vtx
$172.3$ ${}^{+10.8}_{-9.6}$ $\pm10.8$ 69
AALTONEN
2007B
 CDF ${}\geq{}$4 jets (${{\mathit b}}$-tag)
$174.0$ $\pm2.2$ $\pm4.8$ 70
AALTONEN
2007D
 CDF ${}\geq{}$6 jets, vtx ${{\mathit b}}$-tag
$170.8$ $\pm2.2$ $\pm1.4$ 71, 72
AALTONEN
2007I
 CDF lepton + jets (${{\mathit b}}$-tag)
$173.7$ $\pm4.4$ ${}^{+2.1}_{-2.0}$ 73, 68
ABAZOV
2007F
 D0 lepton + jets
$176.2$ $\pm9.2$ $\pm3.9$ 74
ABAZOV
2007W
 D0 dilepton (MWT)
$179.5$ $\pm7.4$ $\pm5.6$ 74
ABAZOV
2007W
 D0 dilepton (${{\mathit \nu}}$WT)
$164.5$ $\pm3.9$ $\pm3.9$ 75, 72
ABULENCIA
2007D
 CDF dilepton
$180.7$ ${}^{+15.5}_{-13.4}$ $\pm8.6$ 76
ABULENCIA
2007J
 CDF lepton + jets
$170.3$ ${}^{+4.1}_{-4.5}$ ${}^{+1.2}_{-1.8}$ 77, 72
ABAZOV
2006U
 D0 lepton + jets (${{\mathit b}}$-tag)
$173.2$ ${}^{+2.6}_{-2.4}$ $\pm3.2$ 78, 79
ABULENCIA
2006D
 CDF lepton + jets
$173.5$ ${}^{+3.7}_{-3.6}$ $\pm1.3$ 78, 65
ABULENCIA
2006D
 CDF lepton + jets
$165.2$ $\pm6.1$ $\pm3.4$ 80, 72
ABULENCIA
2006G
 CDF dilepton
$170.1$ $\pm6.0$ $\pm4.1$ 81, 65
ABULENCIA
2006V
 CDF dilepton
$178.5$ $\pm13.7$ $\pm7.7$ 82, 83
ABAZOV
2005
D0 6 or more jets
$180.1$ $\pm3.6$ $\pm3.9$ 84, 85
ABAZOV
2004G
 D0 lepton + jets
$176.1$ $\pm5.1$ $\pm5.3$ 86
AFFOLDER
2001
CDF lepton + jets
$176.1$ $\pm6.6$ 87
AFFOLDER
2001
CDF dilepton, lepton+jets, all-jets
$172.1$ $\pm5.2$ $\pm4.9$ 88
ABBOTT
1999G
 D0 di-lepton, lepton+jets
$176.0$ $\pm6.5$ 89, 90
ABE
1999B
 CDF dilepton, lepton+jets, all-jets
$167.4$ $\pm10.3$ $\pm4.8$ 91, 90
ABE
1999B
 CDF dilepton
$168.4$ $\pm12.3$ $\pm3.6$ 85
ABBOTT
1998D
 D0 dilepton
$173.3$ $\pm5.6$ $\pm5.5$ 92, 85
ABBOTT
1998F
 D0 lepton + jets
$175.9$ $\pm4.8$ $\pm5.3$ 91, 93
ABE
1998E
 CDF lepton + jets
$161$ $\pm17$ $\pm10$ 91
ABE
1998F
 CDF dilepton
$172.1$ $\pm5.2$ $\pm4.9$ 94
BHAT
1998B
 RVUE dilepton and lepton+jets
$173.8$ $\pm5.0$ 95
BHAT
1998B
 RVUE dilepton, lepton+jets, all-jets
$173.3$ $\pm5.6$ $\pm6.2$ 85
ABACHI
1997E
 D0 lepton + jets
$186$ $\pm10$ $\pm5.7$ 96, 91
ABE
1997R
 CDF 6 or more jets
$199$ ${}^{+19}_{-21}$ $\pm22$
ABACHI
1995
D0 lepton $+$ jets
$176$ $\pm8$ $\pm10$
ABE
1995F
 CDF lepton $+$ ${{\mathit b}}$-jet
$174$ $\pm10$ ${}^{+13}_{-12}$
ABE
1994E
 CDF lepton $+$ ${{\mathit b}}$-jet
1  HAYRAPETYAN 2024F based on up to 5 and 20 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 7 and 8 TeV, respectively. The combination includes 15 input measurements in ${{\mathit t}}{{\overline{\mathit t}}}$ events that exploit both semileptonic and hadronic decays of the top quark as well as ${{\mathit t}}$-channel single-top events.
2  AAD 2023N based on 36.1 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. The second error is the sum of systematic ($\pm0.66$) and that from changing parton-shower gluon recoil scheme ($\pm0.25$) uncertainties. The distribution of the invariant mass ${\mathit m}_{\mathrm {{{\mathit \ell}} {{\mathit \mu}}}}$ (${{\mathit \ell}}$ from ${{\mathit W}}$ and ${{\mathit \mu}}$ from ${{\mathit b}}$-hadron decay) is used, which is less sensitive to jet energy uncertainties and top production modelling.
3  TUMASYAN 2023BB based on 36.3 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. For each event, the mass is reconstructed from a kinematic fit of the decay products to a ${{\mathit t}}{{\overline{\mathit t}}}$ hypothesis. A profile likelihood method is applied using up to four observables per event.
4  TUMASYAN 2023Z based on 138 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. The second error is the sum of experimental ($\pm{}$0.61), model ($\pm{}$0.47), and theoretical ($\pm{}$0.23) uncertainties. The products of the hadronic decay of a top quark with $p_T$ $>$ 400 GeV, in the ${{\mathit \ell}}$ + jets channel of ${{\mathit t}}{{\overline{\mathit t}}}$, are reconstructed as a single jet. The top quark mass is determined from the normalized differential cross section measurement in the ${\mathit m}_{\mathrm {jet}}$ distribution.
5  TUMASYAN 2021G based on 35.9 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. Events are selected by requiring 1${{\mathit \ell}}$ + 2jets(1${{\mathit b}}$ jet) final state.
6  SIRUNYAN 2020AR based on 35.9 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. The products of the hadronic decay of a top quark with $p_T$ $>$ 400 GeV, in the ${{\mathit \ell}}$ + jets channel of ${{\mathit t}}{{\overline{\mathit t}}}$ are reconstructed as a single jet. The top quark mass is determined from the normalized differential cross section measurement in the ${\mathit m}_{\mathrm {jet}}$ distribution.
7  SIRUNYAN 2019AP based on 35.9 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. A kinematical fit is applied to each event assuming the signal event topology. ${\mathit m}_{{{\mathit t}}}$ is determined simultaneously with a jet energy scale factor (JSF). The second error represents stat.+JSF. Modeling uncertainties are larger than in the measurements at $\sqrt {s }$ = 7 and 8 TeV because of the use of new alternative color reconnection models.
8  SIRUNYAN 2019AR based on 35.9 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. Obtained from a simultaneous fit of the cross section and the top quark mass in the POWHEG simulation. The cross section is used also to extract the $\overline{\rm{}MS}$ mass and the strong coupling constant for different PDF sets.
9  TEVEWWG 2016 is the latest Tevatron average (July 2016) provided by the Tevatron Electroweak Working Group. It takes correlated uncertainties into account and has a ${{\mathit \chi}^{2}}$ of 10.8 for 11 degrees of freedom.
10  AABOUD 2019AC based on 20.2 fb${}^{-1}$ in ${{\mathit p}}{{\mathit p}}$ collisions at $\sqrt {s }$ = 8 TeV. Uses optimized event selection to suppress less-well-reconstructed events and template fits to determine ${\mathit m}_{{{\mathit t}}}$ together with a global jet energy scale factor and a relative ${{\mathit b}}$-to-light-jet energy scale factor.
11  AABOUD 2019AC is an ATLAS combination of 7 and 8 TeV top-quark mass determination in the dilepton, lepton + jets, and all jets channels.
12  SIRUNYAN 2019AP based on 35.9 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. A combined measurement using the lepton+jets and all-jets channels through a single likelihood function. See SIRUNYAN 2018DE.
13  SIRUNYAN 2018DE based on 35.9 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 13 TeV. ${\mathit m}_{{{\mathit t}}}$ is determined simultaneously with an overall jet energy scale factor constrained by the mass of the hadronically decayed ${{\mathit W}}$. Compared to the Run 1 analysis a more advanced treatment of modeling uncertainties are employed, in particular concerning color-reconnection models. Superseded by TUMASYAN 2023BB.
14  AABOUD 2017AH based on 20.2 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 8 TeV. Uses template fits to the ratio of the masses of three-jets (from ${{\mathit t}}$ candidate) and dijets (from ${{\mathit W}}$ candidate), to suppress jet energy scale uncertainty. Large QCD background is modelled using a data-driven method.
15  ABAZOV 2017B is a combination of measurements of the top quark mass by D0 in the lepton+jets and dilepton channels, using all data collected in Run I ($1992 - 1996$) at $\sqrt {s }$ = 1.8 TeV and Run II ($2001 - 2011$) at $\sqrt {s }$ = 1.96 TeV of the Tevatron, corresponding to integrated luminosities of 0.1 ${\mathrm {fb}}{}^{-1}$ and 9.7 ${\mathrm {fb}}{}^{-1}$, respectively.
16  SIRUNYAN 2017L based on 19.7 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 8 TeV. ${\mathit m}_{{{\mathit t}}}$ is reconstructed from a fit to the invariant mass distribution of ${{\mathit \mu}}{{\mathit \nu}}{{\mathit b}}$, where ${{\mathit p}_{{{T}}}^{miss}}$ and ${{\mathit W}}$ mass constraint are used to reconstruct ${{\mathit \nu}}$ momentum. The number of events for various contributions, except for the ${{\mathit t}}$-channel single top one, are fixed to the values extracted from simulation. Superseded by TUMASYAN 2021G.
17  SIRUNYAN 2017N based on 19.7 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 8 TeV. The fully hadronic decay of a highly-boosted ${{\mathit t}}$ is reconstructed in the ${{\mathit \ell}}$+jets channel and unfolded at the particle level. The sensitivity of the peak position of the ${{\mathit m}_{{{jet}}}}$ distribution is used to test quality of the modelling by the simulation.
18  SIRUNYAN 2017O based on 19.7 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 8 TeV. Analysis is based on the kinematical observables $\mathit M({{\mathit b}}{{\mathit \ell}}$), ${{\mathit M}_{{{T2}}}}$ and $\mathit M({{\mathit b}}{{\mathit \ell}}{{\mathit \nu}}$). A fit is performed to determine ${\mathit m}_{{{\mathit t}}}$ and an overall jet energy scale factor simultaneously.
19  AABOUD 2016T based on 20.2 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 8 TeV. The analysis is refined using the ${{\mathit p}_{{{T}}}}$ and invariant mass distributions of ${{\mathit \ell}}+{{\mathit b}}$-jet system. A combination with measurements from $\sqrt {s }$ = 7 TeV data in the dilepton and lepton+jets channels gives $172.84$ $\pm0.34$ $\pm0.61$ GeV.
20  AABOUD 2016T is an ATLAS combination of 8 TeV top-quark mass in the dilepton channel with previous measurements from $\sqrt {s }$ = 7 TeV data in the dilepton and lepton + jets channels.
21  ABAZOV 2016 based on 9.7 fb${}^{-1}$ of data in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. Employs improved fit to minimize statistical errors and improved jet energy calibration, using lepton + jets mode, which reduces error of jet energy scale. Based on previous determination in ABAZOV 2012AB with increased integrated luminosity and improved fit and calibrations.
22  ABAZOV 2016D based on 9.7 fb${}^{-1}$ of data in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV, using the matrix element technique. Based on previous determination in ABAZOV 2011R with increased integrated luminosity. There is a strong correlation with the determination in ABAZOV 2016. (See ABAZOV 2017B.)
23  KHACHATRYAN 2016AK based on 19.7 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 8 TeV. Combination of the three top mass measurements in KHACHATRYAN 2016AK and with the CMS results at $\sqrt {s }$ = 7 TeV gives $172.44$ $\pm0.13$ $\pm0.47$ GeV.
24  The top mass and jet energy scale factor are determined by a fit.
25  Uses the analytical matrix weighting technique method.
26  KHACHATRYAN 2016AK based on 19.7 ${\mathrm {fb}}{}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 8 TeV. Combination of the three top mass measurements in KHACHATRYAN 2016AK and with the CMS results at $\sqrt {s }$ = 7 TeV.
27  KHACHATRYAN 2016AL based on 19.7 fb${}^{-1}$ in ${{\mathit p}}{{\mathit p}}$ collisions at $\sqrt {s }$ = 8 TeV. Determined from the invariant mass distribution of leptons and reconstructed secondary vertices from ${{\mathit b}}$ decays using only charged particles. The uncertainty is dominated by modeling of ${{\mathit b}}$ fragmentation and top ${{\mathit p}_{{{T}}}}$ distribution.
28  KHACHATRYAN 2016CB based on 666 candidate reconstructed events corresponding to 19.7 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 8 TeV. The measurement exploits correlation of ${\mathit m}_{{{\mathit t}}}$ with M(${{\mathit J / \psi}}{{\mathit \ell}}$) in the same top quark decay, using a high-purity event sample. A study on modeling of ${{\mathit b}}$-quark fragmentation is given in Sec.3.3.
29  AAD 2015AW based on 4.6 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 7 TeV. Uses template fits to the ratio of the masses of three-jets (from ${{\mathit t}}$ candidate) and dijets (from ${{\mathit W}}$ candidate). Large background from multijet production is modeled with data-driven methods.
30  AAD 2015BF based on 4.6 fb${}^{-1}$ in ${{\mathit p}}{{\mathit p}}$ collisions at $\sqrt {s }$ = 7 TeV. Using a three-dimensional template likelihood technique the lepton plus jets (${}\geq{}1{{\mathit b}}$-tagged) channel gives $172.33$ $\pm0.75$ $\pm1.02$ GeV, while exploiting a one dimensional template method using ${\mathit m}_{{{\mathit \ell}} {{\mathit b}}}$ the dilepton channel (1 or 2${{\mathit b}}$-tags) gives $173.79$ $\pm0.54$ $\pm1.30$ GeV. The results are combined.
31  AALTONEN 2015D based on 9.1 fb${}^{-1}$ of ${{\mathit p}}{{\overline{\mathit p}}}$ data at $\sqrt {s }$ = 1.96 TeV. Uses a template technique to fit a distribution of a variable defined by a linear combination of variables sensitive and insensitive to jet energy scale to optimize reduction of systematic errors. ${{\mathit b}}$-tagged and non-${{\mathit b}}$-tagged events are separately analyzed and combined.
32  Based on 9.3 fb${}^{-1}$ of ${{\mathit p}}{{\overline{\mathit p}}}$ data at $\sqrt {s }$ = 1.96 TeV. Multivariate algorithm is used to discriminate signal from backgrounds, and templates are used to measure ${\mathit m}_{{{\mathit t}}}$.
33  Based on 9.7 fb${}^{-1}$ of ${{\mathit p}}{{\overline{\mathit p}}}$ data at $\sqrt {s }$ = 1.96 TeV. A matrix element method is used to calculate the probability of an event to be signal or background, and the overall jet energy scale is constrained $\mathit in~situ$ by ${\mathit m}_{{{\mathit W}}}$. See ABAZOV 2015G for further details.
34  Based on 3.54 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 7 TeV. The mass is reconstructed for each event employing a kinematic fit of the jets to a ttbar hypothesis. The combination with the pervious CMS measurements in the dilepton and the lepton+jets channels gives $173.54$ $\pm0.33$ $\pm0.96$ GeV.
35  Based on 8.7 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. Events with an identified charged lepton or small $\not E_T$ are rejected from the event sample, so that the measurement is statistically independent from those in the ${{\mathit \ell}}$ + jets and all hadronic channels while being sensitive to those events with a ${{\mathit \tau}}$ lepton in the final state.
36  Based on 5.0 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 7 TeV. CHATRCHYAN 2013S studied events with di-lepton + $\not E_T$ + ${}\geq{}$2 ${{\mathit b}}$-jets, and looked for kinematical endpoints of MT2, MT2$_{T}$, and subsystem variables.
37  AAD 2012I based on 1.04 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 7 TeV. Uses 2d-template analysis (MT) with ${\mathit m}_{{{\mathit t}}}$ and jet energy scale factor (JSF) from ${\mathit m}_{{{\mathit W}}}$ mass fit.
38  Based on 8.7 fb${}^{-1}$ of data in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at 1.96 TeV. The JES is calibrated by using the dijet mass from the ${{\mathit W}}$ boson decay.
39  Use the ME method based on 2.2 fb${}^{-1}$ of data in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at 1.96 TeV.
40  Combination based on up to 5.8 fb${}^{-1}$ of data in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at 1.96 TeV.
41  Based on 5.8 fb${}^{-1}$ of data in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at 1.96 TeV the quoted value is ${\mathit m}_{{{\mathit t}}}$ = $172.5$ $\pm1.4$(stat)$\pm1.0(JES)\pm1.1$(syst) GeV. The measurement is performed with a liklihood fit technique which simultaneously determines ${\mathit m}_{{{\mathit t}}}$ and JES (Jet Energy Scale).
42  Based on 4.3 fb${}^{-1}$ of data in p-pbar collisions at 1.96 TeV. The measurement reduces the JES uncertainty by using the single lepton channel study of ABAZOV 2011P.
43  Combination with the result in 1 fb${}^{-1}$ of preceding data reported in ABAZOV 09AH as well as the MWT result of ABAZOV 2011R with a statistical correlation of 60$\%$.
44  Based on 5.0 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 7 TeV. Uses an analytical matrix weighting technique (AMWT) and full kinematic analysis (KIN).
45  Based on 5.0 fb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ data at $\sqrt {s }$ = 7 TeV. The first error is statistical and JES combined, and the second is systematic. Ideogram method is used to obtain 2D liklihood for the kinematical fit with two parameters mtop and JES.
46  Based on 3.2 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. The first error is from statistics and JES combined, and the latter is from the other systematic uncertainties. The result is obtained using an unbinned maximum likelihood method where the top quark mass and the JES are measured simultaneously, with ${{\mathit \Delta}_{{{JES}}}}$ = $0.3$ $\pm0.3$(stat).
47  Based on 5.7 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. Events with an identified charged lepton or small $\not E_T$ are rejected from the event sample, so that the measurement is statistically independent from those in the ${{\mathit \ell}}$ + jets and all hadronic channels while being sensitive to those events with a ${{\mathit \tau}}$ lepton in the final state. Supersedes AALTONEN 2007B.
48  AALTONEN 2011E based on 5.6 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. Employs a multi-dimensional template likelihood technique where the lepton plus jets (one or two ${{\mathit b}}$-tags) channel gives $172.2$ $\pm1.2$ $\pm0.9$ GeV while the dilepton channel yields $170.3$ $\pm2.0$ $\pm3.1$ GeV. The results are combined. OUR EVALUATION includes the measurement in the dilepton channel only.
49  Uses a likelihood fit of the lepton $p_T$ distribution based on 2.7 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV.
50  Based on 3.6 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. ABAZOV 2011P reports $174.94$ $\pm0.83$ $\pm0.78$ $\pm0.96$ GeV, where the first uncertainty is from statistics, the second from JES, and the last from other systematic uncertainties. We combine the JES and systematic uncertainties. A matrix-element method is used where the JES uncertainty is constrained by the ${{\mathit W}}$ mass. ABAZOV 2011P describes a measurement based on 2.6 fb${}^{-1}$ that is combined with ABAZOV 2008AH, which employs an independent 1 fb${}^{-1}$ of data.
51  Based on a matrix-element method which employs 5.4 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. Superseded by ABAZOV 2012AB.
52  Based on 36 pb${}^{-1}$ of ${{\mathit p}}{{\mathit p}}$ collisions at $\sqrt {s }$ = 7 TeV. A Kinematic Method using ${{\mathit b}}$-tagging and an analytical Matrix Weighting Technique give consistent results and are combined. Superseded by CHATRCHYAN 2012BA.
53  Based on 5.6 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. The likelihood calculated using a matrix element method gives ${\mathit m}_{{{\mathit t}}}$ = $173.0$ $\pm0.7$(stat)$\pm0.6(JES)\pm0.9$(syst) GeV, for a total uncertainty of 1.2 GeV.
54  Based on 3.4 fb${}^{-1}$ of ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. The result is obtained by combining the MT2 variable method and the NWA (Neutrino Weighting Algorithm). The MT2 method alone gives ${\mathit m}_{{{\mathit t}}}$ = $168.0$ ${}^{+4.8}_{-4.0}$(stat)$\pm2.9$(syst) GeV with smaller systematic error due to small JES uncertainty.
55  Based on 1.9 fb${}^{-1}$ in ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. The result is from the measurement using the transverse decay length of ${{\mathit b}}$-hadrons and that using the transverse momentum of the ${{\mathit W}}$ decay muons, which are both insensitive to the JES (jet energy scale) uncertainty. OUR EVALUATION uses only the measurement exploiting the decay length significance which yields $166.9$ ${}^{+9.5}_{-8.5}$(stat)$\pm2.9$ (syst) GeV. The measurement that uses the lepton transverse momentum is excluded from the average because of a statistical correlation with other samples.
56  Based on 2.9 fb${}^{-1}$ of ${{\mathit p}}{{\overline{\mathit p}}}$ collisions at $\sqrt {s }$ = 1.96 TeV. The first error is from statistics and JES uncertainty, and the latter is from the other systematics. Neural-network-based kinematical selection of 6 highest $\mathit E_{T}$ jets with a vtx ${{\mathit b}}$-tag is used to distinguish signal from background. Superseded by AALTONEN 2012G.
57  Based on 2 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The top mass is obtained from the measurement of the invariant mass of the lepton (${{\mathit e}}$ or ${{\mathit \mu}}$) from ${{\mathit W}}$ decays and the soft ${{\mathit \mu}}$ in ${{\mathit b}}$-jet. The result is insensitive to jet energy scaling.
58  Based on 1.9 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The first error is from statistics and jet energy scale uncertainty, and the latter is from the other systematics. Matrix element method with effective propagators.
59  Based on 943 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The first error is from statistical and jet-energy-scale uncertainties, and the latter is from other systematics. AALTONEN 2009K selected 6 jet events with one or more vertex ${{\mathit b}}$-tags and used the tree-level matrix element to construct template models of signal and background.
60  Based on 1.9 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The first error is from statistical and jet-energy-scale (JES) uncertainties, and the second is from other systematics. Events with lepton + jets and those with dilepton + jets were simultaneously fit to constrain ${\mathit m}_{{{\mathit t}}}$ and JES. Lepton + jets data only give ${\mathit m}_{{{\mathit t}}}$ = $171.8$ $\pm2.2$ GeV, and dilepton data only give ${\mathit m}_{{{\mathit t}}}$ = $171.2$ ${}^{+5.3}_{-5.1}$ GeV.
61  Based on 2 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. Matrix Element method. Optimal selection criteria for candidate events with two high $p_T$ leptons, high $\not E_T$, and two or more jets with and without ${{\mathit b}}$-tag are obtained by neural network with neuroevolution technique to minimize the statistical error of ${\mathit m}_{{{\mathit t}}}$.
62  Based on 2.9 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. Mass ${\mathit m}_{{{\mathit t}}}$ is estimated from the likelihood for the eight-fold kinematical solutions in the plane of the azimuthal angles of the two neutrino momenta.
63  Based on 1 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. Events with two identified leptons, and those with one lepton plus one isolated track and a ${{\mathit b}}$-tag were used to constrain ${\mathit m}_{{{\mathit t}}}$. The result is a combination of the ${{\mathit \nu}}$WT (${{\mathit \nu}}$ Weighting Technique) result of $176.2$ $\pm4.8$ $\pm2.1$ GeV and the MWT (Matrix-element Weighting Technique) result of $173.2$ $\pm4.9$ $\pm2.0$ GeV.
64  Reports measurement of $170.7$ ${}^{+4.2}_{-3.9}$ $\pm2.6$ $\pm2.4$ GeV based on 1.2 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The last error is due to the theoretical uncertainty on $\sigma _{{{\mathit t}} {{\overline{\mathit t}}}}$. Without the cross-section constraint a top mass of $169.7$ ${}^{+5.2}_{-4.9}$ $\pm3.1$ GeV is obtained.
65  Template method.
66  Result is based on 1 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The first error is from statistics and jet energy scale uncertainty, and the latter is from the other systematics.
67  Based on 310 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV.
68  Ideogram method.
69  Based on 311 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. Events with 4 or more jets with $\mathit E_{T}>$ 15 GeV, significant missing $\mathit E_{T}$, and secondary vertex ${{\mathit b}}$-tag are used in the fit. About 44$\%$ of the signal acceptance is from ${{\mathit \tau}}{{\mathit \nu}}$ + 4 jets. Events with identified ${{\mathit e}}$ or ${{\mathit \mu}}$ are vetoed to provide a statistically independent measurement.
70  Based on 1.02 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. Superseded by AALTONEN 2012G.
71  Based on 955 pb${}^{-1}$ of data $\sqrt {s }$ = 1.96 TeV. ${\mathit m}_{{{\mathit t}}}$ and JES (Jet Energy Scale) are fitted simultaneously, and the first error contains the JES contribution of 1.5 GeV.
72  Matrix element method.
73  Based on 425 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The first error is a combination of statistics and JES (Jet Energy Scale) uncertainty, which has been measured simultaneously to give JES = $0.989$ $\pm0.029$(stat).
74  Based on 370 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. Combined result of MWT (Matrix-element Weighting Technique) and ${{\mathit \nu}}$WT (${{\mathit \nu}}$ Weighting Technique) analyses is $178.1$ $\pm6.7$ $\pm4.8~$GeV.
75  Based on 1.0 fb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. ABULENCIA 2007D improves the matrix element description by including the effects of initial-state radiation.
76  Based on 695 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The transverse decay length of the ${\mathit {\mathit b}}$ hadron is used to determine ${\mathit m}_{{{\mathit t}}}$, and the result is free from the JES (jet energy scale) uncertainty.
77  Based on $\sim{}$400 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV. The first error includes statistical and systematic jet energy scale uncertainties, the second error is from the other systematics. The result is obtained with the ${{\mathit b}}$-tagging information. The result without ${{\mathit b}}$-tagging is $169.2$ ${}^{+5.0}_{-7.4}{}^{+1.5}_{-1.4}$ GeV. Superseded by ABAZOV 2008AH.
78  Based on 318 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV.
79  Dynamical likelihood method.
80  Based on 340 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV.
81  Based on 360 pb${}^{-1}$ of data at $\sqrt {s }$ = 1.96 TeV.
82  Based on $110.2$ $\pm5.8$ pb${}^{-1}$ at $\sqrt {s }$ = 1.8~TeV.
83  Based on the all hadronic decays of ${{\mathit t}}{{\overline{\mathit t}}}$ pairs. Single ${{\mathit b}}$-quark tagging via the decay chain ${{\mathit b}}$ $\rightarrow$ ${{\mathit c}}$ $\rightarrow$ ${{\mathit \mu}}$ was used to select signal enriched multijet events. The result was obtained by the maximum likelihood method after bias correction.
84  Obtained by re-analysis of the lepton + jets candidate events that led to ABBOTT 1998F. It is based upon the maximum likelihood method which makes use of the leading order matrix elements.
85  Based on $125$ $\pm7~$pb${}^{-1}$ of data at $\sqrt {\mathit s }$ = $1.8$ TeV.
86  Based on $\sim{}106~$pb${}^{-1}$ of data at $\sqrt {\mathit s }$= $1.8$ TeV.
87  Obtained by combining the measurements in the lepton + jets $\lbrack{}$AFFOLDER 2001], all-jets $\lbrack{}$ABE 1997R, ABE 1999B], and dilepton $\lbrack{}$ABE 1999B] decay topologies.
88  Obtained by combining the D0 result ${\mathit m}_{{{\mathit t}}}$ (GeV) = $168.4$ $\pm12.3$ $\pm3.6$ from 6 di-lepton events (see also ABBOTT 1998D) and ${\mathit m}_{{{\mathit t}}}$ (GeV) = $173.3$ $\pm5.6$ $\pm5.5$ from lepton+jet events (ABBOTT 1998F).
89  Obtained by combining the CDF results of ${\mathit m}_{{{\mathit t}}}$ (GeV)=$167.4$ $\pm10.3$ $\pm4.8$ from 8$~$dilepton events, ${\mathit m}_{{{\mathit t}}}$ (GeV)=$175.9$ $\pm4.8$ $\pm5.3$ from lepton+jet events (ABE 1998E), and ${\mathit m}_{{{\mathit t}}}$ (GeV)=$186.0$ $\pm10.0$ $\pm5.7$ from all-jet events (ABE 1997R). The systematic errors in the latter two measurements are changed in this paper.
90  See AFFOLDER 2001 for details of systematic error re-evaluation.
91  Based on $109$ $\pm7~$pb${}^{-1}$ of data at $\sqrt {\mathit s }$ = $1.8$ TeV.
92  See ABAZOV 2004G.
93  The updated systematic error is listed. See AFFOLDER 2001, appendix$~$C.
94  Obtained by combining the ${D0}$ results of ${\mathit m}_{{{\mathit t}}}$(GeV)=$168.4$ $\pm12.3$ $\pm3.6$ from 6 dilepton events and ${\mathit m}_{{{\mathit t}}}$(GeV)=$173.3$ $\pm5.6$ $\pm5.5$ from 77 lepton+jet events.
95  Obtained by combining the ${D0}$ results from dilepton and lepton+jet events, and the CDF results (ABE 1999B) from dilepton, lepton+jet events, and all-jet events.
96  Based on the first observation of all hadronic decays of ${{\mathit t}}{{\overline{\mathit t}}}$ pairs. Single ${{\mathit b}}$-quark tagging with jet-shape variable constraints was used to select signal enriched multi-jet events. The updated systematic error is listed. See AFFOLDER 2001, appendix$~$C.

           ${{\mathit t}}$-Quark Mass (Direct Measurements) (GeV)
References