${{\mathit \pi}^{\pm}}$ MASS
INSPIRE JSON (beta) PDGID:S008M
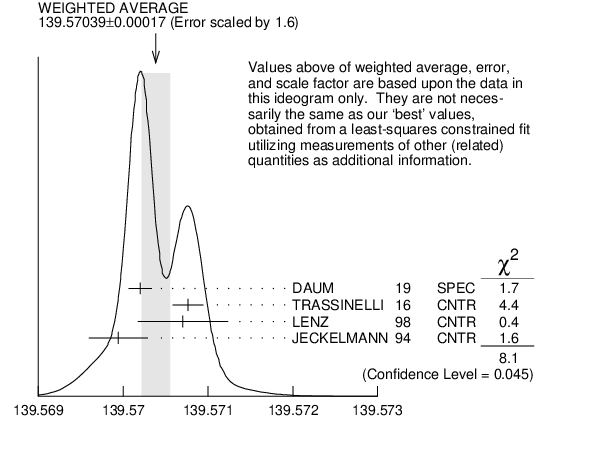
The most accurate charged pion mass measurements are based upon x-ray wavelength measurements for transitions in ${{\mathit \pi}^{-}}$-mesonic atoms. The observed line is the blend of three components, corresponding to different K-shell occupancies. JECKELMANN 1994 revisits the occupancy question, with the conclusion that two sets of occupancy ratios, resulting in two different pion masses (Solutions A and B), are equally probable. We choose the higher Solution$~$B since only this solution is consistent with a positive mass-squared for the muon neutrino, given the precise muon momentum measurements now available (DAUM 1991, ASSAMAGAN 1994, and ASSAMAGAN 1996) for the decay of pions at rest. Earlier mass determinations with pi-mesonic atoms may have used incorrect K-shell screening corrections.
Measurements with an error of $>0.005$ MeV have been omitted from this Listing.
Measurements with an error of $>0.005$ MeV have been omitted from this Listing.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
${{\mathit \pi}^{\pm}}$ mass (MeV) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| References | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Except where otherwise noted, content of the 2025 Review of Particle Physics is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) license. The publication of the Review of Particle Physics is supported by US DOE, MEXT (Japan), INFN (Italy) and CERN. Individual collaborators receive support for their PDG activities from their respective institutes or funding agencies. © 2025. See LBNL disclaimers.