The ${{\mathit W}}$ width listed here corresponds to the width parameter in a Breit-Wigner distribution with mass-dependent width. To obtain the world average, common systematic uncertainties between experiments are properly taken into account. The LEP-2 average ${{\mathit W}}$ width based on published results is $2.195$ $\pm0.083$ GeV [SCHAEL 2013A]. The combined Tevatron data yields an average ${{\mathit W}}$ width of $2.046$ $\pm0.049$ GeV [TEVEWWG 2010]. OUR AVERAGE uses these average LEP and Tevatron width values and combines them together with the ATLAS result, assuming no correlations.

VALUE (GeV) EVTS DOCUMENT ID TECN  COMMENT $\bf{ 2.14 \pm0.05}$ OUR AVERAGE  Error includes scale factor of 1.7.  See the ideogram below. $2.202$ $\pm0.032$ $\pm0.034$ 13.7M 1 AAD 2024 CJ ATLS ${\it{}E}^{\it{}pp}_{\rm{}cm}$ = 7 TeV $2.195$ $\pm0.083$ 2 SCHAEL 2013 A LEP ${\it{}E}^{\it{}ee}_{\rm{}cm}$= $170 - 209$ GeV $2.046$ $\pm0.049$ 3 TEVEWWG 2010 TEVA ${\it{}E}^{\it{}p\overline{\it{}p}}_{\rm{}cm}$ = $1.8 - 1.96$ TeV • • We do not use the following data for averages, fits, limits, etc. • • $2.028$ $\pm0.072$ 5272 4 ABAZOV 2009 AK D0 ${\it{}E}^{\it{}p\overline{\it{}p}}_{\rm{}cm}$ = 1.96 GeV $2.032$ $\pm0.045$ $\pm0.057$ 6055 5 AALTONEN 2008 B CDF ${\it{}E}^{\it{}p\overline{\it{}p}}_{\rm{}cm}$ = 1.96 TeV $2.404$ $\pm0.140$ $\pm0.101$ 10.3k 6 ABDALLAH 2008 A DLPH ${\it{}E}^{\it{}ee}_{\rm{}cm}$= $183 - 209$ GeV $1.996$ $\pm0.096$ $\pm0.102$ 10729 7 ABBIENDI 2006 OPAL ${\it{}E}^{\it{}ee}_{\rm{}cm}$= $170 - 209$ GeV $2.18$ $\pm0.11$ $\pm0.09$ 9795 8 ACHARD 2006 L3 ${\it{}E}^{\it{}ee}_{\rm{}cm}$= $172 - 209$ GeV $2.14$ $\pm0.09$ $\pm0.06$ 8717 9 SCHAEL 2006 ALEP ${\it{}E}^{\it{}ee}_{\rm{}cm}$= $183 - 209$ GeV $2.23$ ${}^{+0.15}_{-0.14}$ $\pm0.10$ 294 10 ABAZOV 2002 E D0 ${\it{}E}^{\it{}p\overline{\it{}p}}_{\rm{}cm}$ = 1.8 TeV $2.152$ $\pm0.066$ 79176 11 ABBOTT 2000 B D0 Extracted value $2.05$ $\pm0.10$ $\pm0.08$ 662 12 AFFOLDER 2000 M CDF ${\it{}E}^{\it{}p\overline{\it{}p}}_{\rm{}cm}$ = 1.8 TeV $2.064$ $\pm0.060$ $\pm0.059$ 13 ABE 1995 W CDF Extracted value $2.10$ ${}^{+0.14}_{-0.13}$ $\pm0.09$ 3559 14 ALITTI 1992 UA2 Extracted value $2.18$ ${}^{+0.26}_{-0.24}$ $\pm0.04$ 15 ALBAJAR 1991 UA1 Extracted value 1  AAD 2024CJ provides an improved determination of the ${{\mathit W}}$ boson mass using the same data as analysed for AABOUD 2018J. In addition, the distributions of the transverse lepton momentum and of the transverse mass are analysed to determine the ${{\mathit W}}$ boson width. 2  SCHAEL 2013A result combines the measurements from the LEP experiments ALEPH (SCHAEL 2006), DELPHI(ABDALLAH 2008A), L3 (ACHARD 2006) and OPAL(ABBIENDI 2006). The average of these four results takes correlations into account and has a ${{\mathit \chi}^{2}}$ probability of 27$\%$. 3  TEVEWWG 2010 result combines the measurements from the Tevtatron experiments CDF (ABE 1995C, AFFOLDER 2000M, AALTONEN 2008B) and D0 (ABAZOV 2002E, ABAZOV 2009AK). The average of these five results takes correlations into account and has a ${{\mathit \chi}^{2}}$ probability of 84$\%$. 4  ABAZOV 2009AK obtain this result fitting the high-end tail (100-200 GeV) of the transverse mass spectrum in ${{\mathit W}}$ $\rightarrow$ ${{\mathit e}}{{\mathit \nu}}$ decays. 5  AALTONEN 2008B obtain this result fitting the high-end tail ($90 - 200$ GeV) of the transverse mass spectrum in semileptonic ${{\mathit W}}$ $\rightarrow$ ${{\mathit e}}{{\mathit \nu}_{{{e}}}}$ and ${{\mathit W}}$ $\rightarrow$ ${{\mathit \mu}}{{\mathit \nu}_{{{\mu}}}}$ decays. 6  ABDALLAH 2008A use direct reconstruction of the kinematics of ${{\mathit W}^{+}}$ ${{\mathit W}^{-}}$ $\rightarrow$ ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit \ell}}{{\mathit \nu}}$ and ${{\mathit W}^{+}}$ ${{\mathit W}^{-}}$ $\rightarrow$ ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit q}}{{\overline{\mathit q}}}$ events. The systematic error includes $\pm0.065$ GeV due to final state interactions. 7  ABBIENDI 2006 use direct reconstruction of the kinematics of ${{\mathit W}^{+}}$ ${{\mathit W}^{-}}$ $\rightarrow$ ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit \ell}}{{\mathit \nu}_{{{{{\mathit \ell}}}}}}$ and ${{\mathit W}^{+}}$ ${{\mathit W}^{-}}$ $\rightarrow$ ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit q}}{{\overline{\mathit q}}}$ events. The systematic error includes $\pm0.003$ GeV due to the uncertainty on the LEP beam energy. 8  ACHARD 2006 use direct reconstruction of the kinematics of ${{\mathit W}^{+}}$ ${{\mathit W}^{-}}$ $\rightarrow$ ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit \ell}}{{\mathit \nu}_{{{{{\mathit \ell}}}}}}$ and ${{\mathit W}^{+}}$ ${{\mathit W}^{-}}$ $\rightarrow$ ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit q}}{{\overline{\mathit q}}}$ events in the C.M. energy range $189 - 209$ GeV. The result quoted here is obtained combining this value of the width with the result obtained from a direct ${{\mathit W}}$ mass reconstruction at 172 and 183 GeV (ACCIARRI 1999). 9  SCHAEL 2006 use direct reconstruction of the kinematics of ${{\mathit W}^{+}}$ ${{\mathit W}^{-}}$ $\rightarrow$ ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit \ell}}{{\mathit \nu}_{{{{{\mathit \ell}}}}}}$ and ${{\mathit W}^{+}}$ ${{\mathit W}^{-}}$ $\rightarrow$ ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit q}}{{\overline{\mathit q}}}$ events. The systematic error includes $\pm0.05$ GeV due to possible effects of final state interactions in the ${{\mathit q}}{{\overline{\mathit q}}}{{\mathit q}}{{\overline{\mathit q}}}$ channel and $\pm0.01$ GeV due to the uncertainty on the LEP beam energy. 10  ABAZOV 2002E obtain this result fitting the high-end tail ($90 - 200$ GeV) of the transverse-mass spectrum in semileptonic ${{\mathit W}}$ $\rightarrow$ ${{\mathit e}}{{\mathit \nu}_{{{e}}}}$ decays. 11  ABBOTT 2000B measure $\mathit R$ = $10.43$ $\pm0.27$ for the ${{\mathit W}}$ $\rightarrow$ ${{\mathit e}}{{\mathit \nu}_{{{e}}}}$ decay channel. They use the SM theoretical predictions for $\sigma\mathrm {({{\mathit W}})}/\sigma\mathrm {({{\mathit Z}})}$ and $\Gamma\mathrm {({{\mathit W}} \rightarrow {{\mathit e}} {{\mathit \nu}_{{{e}}}})}$ and the world average for B(${{\mathit Z}}$ $\rightarrow$ ${{\mathit e}}{{\mathit e}}$). The value quoted here is obtained combining this result ($2.169$ $\pm0.070$ GeV) with that of ABBOTT 1999H. 12  AFFOLDER 2000M fit the high transverse mass ($100 - 200~$GeV) ${{\mathit W}}$ $\rightarrow$ ${{\mathit e}}{{\mathit \nu}_{{{e}}}}$ and ${{\mathit W}}$ $\rightarrow$ ${{\mathit \mu}}{{\mathit \nu}_{{{\mu}}}}$ events to obtain $\Gamma\mathrm {({{\mathit W}})}$= $2.04$ $\pm0.11$(stat)$\pm0.09$(syst) GeV. This is combined with the earlier CDF measurement (ABE 1995C) to obtain the quoted result. 13  ABE 1995W measured $\mathit R$ = $10.90$ $\pm0.32$ $\pm0.29$. They use ${\mathit m}_{{{\mathit W}}}=80.23$ $\pm0.18$ GeV, ${\mathit \sigma (}{{\mathit W}}{)}/{\mathit \sigma (}{{\mathit Z}}{)}$ = $3.35$ $\pm0.03$, $\Gamma\mathrm {({{\mathit W}} \rightarrow {{\mathit e}} {{\mathit \nu}})}$ = $225.9$ $\pm0.9$ MeV, $\Gamma\mathrm {({{\mathit Z}} \rightarrow {{\mathit e}^{+}} {{\mathit e}^{-}})}$ = $83.98$ $\pm0.18$ MeV, and $\Gamma\mathrm {({{\mathit Z}})}$ = $2.4969$ $\pm0.0038$ GeV. 14  ALITTI 1992 measured $\mathit R$ = $10.4$ ${}^{+0.7}_{-0.6}$ $\pm0.3$. The values of ${\mathit \sigma (}{{\mathit Z}}{)}$ and ${\mathit \sigma (}{{\mathit W}}{)}$ come from $\mathit O(\alpha {}^{2}_{\mathit s}$) calculations using ${\mathit m}_{{{\mathit W}}}$ = $80.14$ $\pm0.27$ GeV, and ${\mathit m}_{{{\mathit Z}}}$ = $91.175$ $\pm0.021$ GeV along with the corresponding value of sin$^2\theta _{{{\mathit W}}}$ = $0.2274$. They use ${\mathit \sigma (}{{\mathit W}}{)}/{\mathit \sigma (}{{\mathit Z}}{)}$ = $3.26$ $\pm0.07$ $\pm0.05$ and $\Gamma\mathrm {({{\mathit Z}})}$ = $2.487$ $\pm0.010$ GeV. 15  ALBAJAR 1991 measured $\mathit R$ = $9.5$ ${}^{+1.1}_{-1.0}$ (stat. + syst.). ${\mathit \sigma (}{{\mathit W}}{)}/{\mathit \sigma (}{{\mathit Z}}{)}$ is calculated in QCD at the parton level using ${\mathit m}_{{{\mathit W}}}$ = $80.18$ $\pm0.28$ GeV and ${\mathit m}_{{{\mathit Z}}}$ = $91.172$ $\pm0.031$ GeV along with sin$^2\theta _{\mathit W}$ = $0.2322$ $\pm0.0014$. They use ${\mathit \sigma (}{{\mathit W}}{)}/{\mathit \sigma (}{{\mathit Z}}{)}$ = $3.23$ $\pm0.05$ and $\Gamma\mathrm {({{\mathit Z}})}$ = $2.498$ $\pm0.020$ GeV. This measurement is obtained combining both the electron and muon channels.

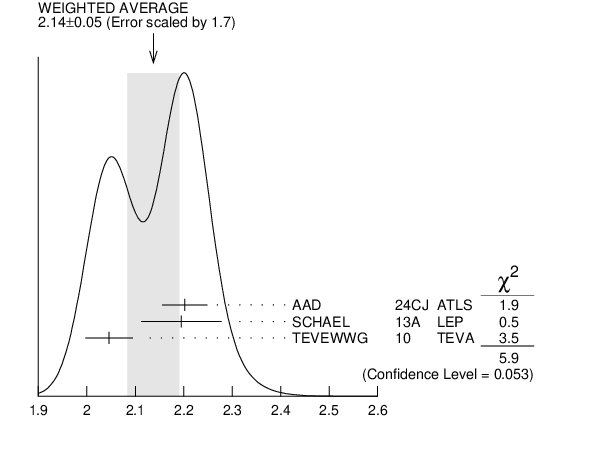
${{\mathit W}}$ WIDTH (GeV)

References