${\it V}_{\it cb}$ MEASUREMENTS

For the discussion of ${\it V}_{\it cb}$ measurements, which is not repeated here, see the review on “Determination of $\vert {\it V}_{\it cb}\vert $ and $\vert {\it V}_{\it ub}\vert $.''
The CKM matrix element $\vert {\it V}_{\it cb}\vert $ can be determined by studying the rate of the semileptonic decay ${{\mathit B}}$ $\rightarrow$ ${{\mathit D}}{}^{(*)}$ ${{\mathit \ell}}{{\mathit \nu}}$ as a function of the recoil kinematics of ${{\mathit D}}{}^{(*)}$ mesons. Taking advantage of theoretical constraints on the normalization and a linear $\omega ~$dependence of the form factors ($\mathit F(\omega $), $\mathit G(\omega $)) provided by Heavy Quark Effective Theory (HQET), the $\vert {\it V}_{\it cb}\vert {\times }\mathit F(\omega $) and $\rho {}^{2}$ can be simultaneously extracted from data, where $\omega $ is the scalar product of the two-meson four velocities, $\mathit F$(1) is the form factor at zero recoil ($\omega $=1) and $\rho {}^{2}$ is the slope. Using the theoretical input of $\mathit F$(1), a value of $\vert {\it V}_{\it cb}\vert $ can be obtained.

$\vert {\it V}_{\it cb}\vert $ ${\times }$ $\mathit F$(1) (from ${{\mathit B}^{0}}$ $\rightarrow$ ${{\mathit D}^{*-}}{{\mathit \ell}^{+}}{{\mathit \nu}}$)

INSPIRE   PDGID:
S052CB1
VALUE ($ 10^{-2} $) DOCUMENT ID TECN  COMMENT
$\bf{ 3.534 \pm0.037}$ OUR EVALUATION  $~~$(Produced by HFLAV) with ${{\mathit \rho}^{2}}=1.139$ $\pm0.020$ and a correlation 0.268. The fitted ${{\mathit \chi}^{2}}$ is 63.2 for 27 degrees of freedom.  See the ideogram below.
$\bf{ 3.60 \pm0.06}$ OUR AVERAGE  Error includes scale factor of 1.5.  See the ideogram below.
$3.676$ $\pm0.028$ $\pm0.086$ 1
ADACHI
2023J
 BELL ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit \Upsilon}{(4S)}}$
$3.64$ $\pm0.09$ 2
PRIM
2023
BELL ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit \Upsilon}{(4S)}}$
$3.506$ $\pm0.015$ $\pm0.056$ 3
WAHEED
2021
BELL ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit \Upsilon}{(4S)}}$
$3.59$ $\pm0.02$ $\pm0.12$ 4
AUBERT
2009A
 BABR ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit \Upsilon}{(4S)}}$
$3.92$ $\pm0.18$ $\pm0.23$ 5
ABDALLAH
2004D
 DLPH ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit Z}^{0}}$
$4.31$ $\pm0.13$ $\pm0.18$ 6
ADAM
2003
CLE2 ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit \Upsilon}{(4S)}}$
$3.55$ $\pm0.14$ ${}^{+0.23}_{-0.24}$ 7
ABREU
2001H
 DLPH ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit Z}}$
$3.71$ $\pm0.10$ $\pm0.20$ 8
ABBIENDI
2000Q
 OPAL ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit Z}}$
$3.19$ $\pm0.18$ $\pm0.19$ 9
BUSKULIC
1997
ALEP ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit Z}}$
• • We do not use the following data for averages, fits, limits, etc. • •
$3.483$ $\pm0.015$ $\pm0.056$ 3
WAHEED
2019
BELL Repl. by WAHEED 2021
$3.46$ $\pm0.02$ $\pm0.10$ 10
DUNGEL
2010
BELL Rep. by WAHEED 2019
$3.59$ $\pm0.06$ $\pm0.14$ 11
AUBERT
2008AT
 BABR Repl. by AUBERT 2009A
$3.44$ $\pm0.03$ $\pm0.11$ 12
AUBERT
2008R
 BABR Repl. by AUBERT 2009A
$3.55$ $\pm0.03$ $\pm0.16$ 13
AUBERT
2005E
 BABR Repl. by AUBERT 2008R
$3.77$ $\pm0.11$ $\pm0.19$ 14
ABDALLAH
2004D
 DLPH ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit Z}^{0}}$
$3.54$ $\pm0.19$ $\pm0.18$ 15
ABE
2002F
 BELL Repl. by DUNGEL 2010
$4.31$ $\pm0.13$ $\pm0.18$ 16
BRIERE
2002
CLE2 ${{\mathit e}^{+}}$ ${{\mathit e}^{-}}$ $\rightarrow$ ${{\mathit \Upsilon}{(4S)}}$
$3.28$ $\pm0.19$ $\pm0.22$
ACKERSTAFF
1997G
 OPAL Repl. by ABBIENDI 2000Q
$3.50$ $\pm0.19$ $\pm0.23$ 17
ABREU
1996P
 DLPH Repl. by ABREU 2001H
$3.51$ $\pm0.19$ $\pm0.20$ 18
BARISH
1995
CLE2 Repl. by ADAM 2003
$3.14$ $\pm0.23$ $\pm0.25$
BUSKULIC
1995N
 ALEP Repl. by BUSKULIC 1997
1  Measured from differential shapes of exclusive ${{\mathit B}}$ $\rightarrow$ ${{\mathit D}^{*}}{{\mathit \ell}^{-}}{{\mathit \nu}_{{{{{\mathit \ell}}}}}}$ (${{\mathit \ell}}$ = ${{\mathit e}}$ or ${{\mathit \mu}}$) decays. Using CNL form factor parametrization and the zero-recoil lattice QCD point $\mathit F$(1) = $0.906$ $\pm0.013$ ADACHI 2023J finds $\vert V_{cb}\vert _{CNL}$ = ($40.57$ $\pm0.31$ $\pm0.95$ $\pm0.58$) $ \times 10^{-3}$ where the last uncertainty is due to the prediction of $\mathit F$(1). Also reports a measurement of $\vert V_{cb}\vert _{BGL}$ = ($40.13$ $\pm0.27$ $\pm0.93$ $\pm0.58$) $ \times 10^{-3}$ using BGL form factors parametrization.
2  Measured from differential shapes of exclusive ${{\mathit B}}$ $\rightarrow$ ${{\mathit D}^{*}}{{\mathit \ell}^{-}}{{\mathit \nu}_{{{{{\mathit \ell}}}}}}$ decays with hadronic tag-side reconstruction and extracting the CNL and BGL form factor parameters. PRIM 2023 finds $\vert V_{cb}\vert _{CNL}$ = ($40.2$ $\pm0.9$) $ \times 10^{-3}$ with the zero-recoil lattice QCD point $\mathit F$(1) = $0.906$ $\pm0.013$. PRIM 2023 provides also a measurement of $\vert V_{cb}\vert _{BGL}$ = ($40.7$ $\pm1.0$) $ \times 10^{-3}$.
3  WAHEED 2021 uses fully reconstructed ${{\mathit D}^{*-}}{{\mathit \ell}^{+}}{{\mathit \nu}}$ events (${{\mathit \ell}}$ = ${{\mathit e}}$ or ${{\mathit \mu}}$) and ${{\mathit \eta}_{{{EW}}}}$ = 1.0066.
4  Obtained from a global fit to ${{\mathit B}}$ $\rightarrow$ ${{\mathit D}^{(*)}}{{\mathit \ell}}{{\mathit \nu}_{{{{{\mathit \ell}}}}}}$ events, with reconstructed ${{\mathit D}^{0}}{{\mathit \ell}}$ and ${{\mathit D}^{+}}{{\mathit \ell}}$ final states and $\rho {}^{2}$ = $1.22$ $\pm0.02$ $\pm0.07$.
5  Measurement using fully reconstructed ${{\mathit D}^{*}}$ sample with a $\rho {}^{2}$ = $1.32$ $\pm0.15$ $\pm0.33$.
6  Average of the ${{\mathit B}^{0}}$ $\rightarrow$ ${{\mathit D}^{*}{(2010)}^{-}}{{\mathit \ell}^{+}}{{\mathit \nu}}$ and ${{\mathit B}^{+}}$ $\rightarrow$ ${{\overline{\mathit D}}^{*}{(2007)}}$) ${{\mathit \ell}^{+}}{{\mathit \nu}}$ modes with $\rho {}^{2}$ = $1.61$ $\pm0.09$ $\pm0.21$ and $\mathit f_{+−}$ = $0.521$ $\pm0.012$.
7  ABREU 2001H measured using about 5000 partial reconstructed ${{\mathit D}^{*}}$ sample with a $\rho {}^{2}=1.34$ $\pm0.14$ ${}^{+0.24}_{-0.22}$.
8  ABBIENDI 2000Q: measured using both inclusively and exclusively reconstructed ${{\mathit D}^{*\pm}}$ samples with a $\rho {}^{2}=1.21$ $\pm0.12$ $\pm0.20$. The statistical and systematic correlations between $\vert {\it V}_{\it cb}\vert {\times }\mathit F$(1) and $\rho {}^{2}$ are $0.90$ and $0.54$ respectively.
9  BUSKULIC 1997: measured using exclusively reconstructed ${{\mathit D}^{*\pm}}$ with a $\mathit a{}^{2}=0.31$ $\pm0.17$ $\pm0.08$. The statistical correlation is $0.92$.
10  Uses fully reconstructed ${{\mathit D}^{*-}}{{\mathit \ell}^{+}}{{\mathit \nu}}$ events (${{\mathit \ell}}$ = ${{\mathit e}}$ or ${{\mathit \mu}}$).
11  Measured using the dependence of ${{\mathit B}^{-}}$ $\rightarrow$ ${{\mathit D}^{*0}}{{\mathit e}^{-}}{{\overline{\mathit \nu}}_{{{e}}}}$ decay differential rate and the form factor description by CAPRINI 1998 with $\rho {}^{2}$ = $1.16$ $\pm0.06$ $\pm0.08$.
12  Measured using fully reconstructed ${{\mathit D}^{*}}$ sample and a simultaneous fit to the Caprini-Lellouch-Neubert form factor parameters: $\rho {}^{2}$ = $1.191$ $\pm0.048$ $\pm0.028$, $\mathit R_{1}$(1) = $1.429$ $\pm0.061$ $\pm0.044$, and $\mathit R_{2}$(1) = $0.827$ $\pm0.038$ $\pm0.022$.
13  Measurement using fully reconstructed ${{\mathit D}^{*}}$ sample with a $\rho {}^{2}$ = $1.29$ $\pm0.03$ $\pm0.27$.
14  Combines with previous partial reconstructed ${{\mathit D}^{*}}$ measurement with a $\rho {}^{2}$ = $1.39$ $\pm0.10$ $\pm0.33$.
15  Measured using exclusive ${{\mathit B}^{0}}$ $\rightarrow$ ${{\mathit D}^{*}{(892)}^{-}}{{\mathit e}^{+}}{{\mathit \nu}}$ decays with $\rho {}^{2}$= $1.35$ $\pm0.17$ $\pm0.19$ and a correlation of $0.91$.
16  BRIERE 2002 result is based on the same analysis and data sample reported in ADAM 2003.
17  ABREU 1996P: measured using both inclusively and exclusively reconstructed ${{\mathit D}^{*\pm}}$ samples.
18  BARISH 1995: measured using both exclusive reconstructed ${{\mathit B}^{0}}$ $\rightarrow$ ${{\mathit D}^{*-}}{{\mathit \ell}^{+}}{{\mathit \nu}}$ and ${{\mathit B}^{+}}$ $\rightarrow$ ${{\mathit D}^{*0}}{{\mathit \ell}^{+}}{{\mathit \nu}}$ samples. They report their experiment's uncertainties $\pm{}0.0019$ $\pm0.0018$ $\pm0.0008$, where the first error is statistical, the second is systematic, and the third is the uncertainty in the lifetimes. We combine the last two in quadrature.

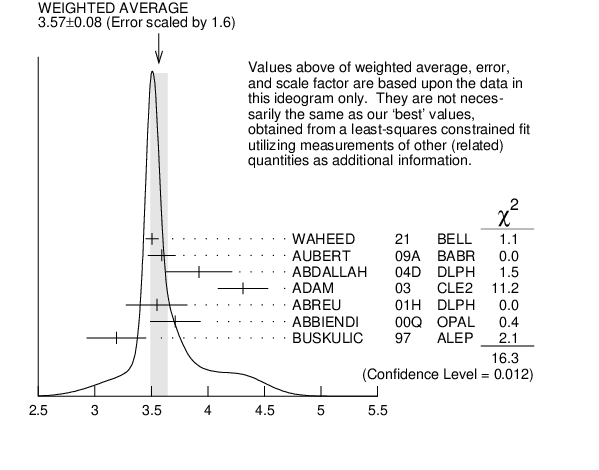
           $\vert {\it V}_{\it cb}\vert $ ${\times }$ $\mathit F$(1) (from ${{\mathit B}^{0}}$ $\rightarrow$ ${{\mathit D}^{*-}}{{\mathit \ell}^{+}}{{\mathit \nu}}$)
References